1、推导pV=nRT V=fp,T,N求V全微分 不定积分得到lnV+lnp=lnT+C 令C=lnR 即得pVm=RT 同乘以n得到pV=nRT 注所有气体R值均相同如果压强温度和体积都采用国际单位SI,则P表示压强,单位PaV表示气体体积,单位立方米n表示物质的量,单位molT表示热力学温度,单位K开尔文R表。
2、具体推导过程如下阿伏加德罗定律研究的是理想气体,故应用理想气体状态方程 既PV=nRT 其中P为压强V为气体体积n为物质的量对应分子数R为一个常数T为热力学温度 得到PV=nRT,其中R为常数 故剩余4个变量,知道两个,既知道另外两个的关系 得到推论12再根据n=,带入PV=nRT。
3、V=Mρ,代入PV=nRT中,由于n是摩尔量,当n为单位1时,就是推出PM=ρRT了。
4、编辑本段公式pV=nRT克拉伯龙方程1 p为气体压强,单位PaV为气体体积,单位m3n为气体的物质的量,单位mol,T为体系温度,单 理想气体状态方程位K R为比例系数,数值不同状况下有所不同,单位是Jmol·K 在摩尔表示的状态方程中,R为比例常数,对任意理想气体而言,R是一定的。
5、因为n=mM ρ=mvn物质的量m物质的质量,M物质的摩尔质量,数值上等于物质的分量,气态物质的密度,所以克拉伯龙方程式也可写成以下两种形式pv=mRTM和pM=ρRT 即n=mM,m×TM=M×n×TM=nT,其实就是消掉了大M。
6、我解答查理定律吧先建立一个不能通过物质但体积会随物质膨胀而膨胀的箱子,设箱子里只有一摩的气体,并且当时有一个单位的体积,当P不变T升高时,V变大当T不变,P升高时,V变小所以,为了使n,v不变,T升高P也要升高,所以成正比这是我的思路。
7、公式含义克拉伯龙方程PV=nRT描述了理想气体的状态,其中P代表压强,V为气体体积,n表示物质的量,T是绝对温度,R是气体常数气体常数R在国际单位制下,R的值约为8314帕·米#179摩尔·K在不同的单位体系下,R的值会有所调整公式应用压强体积温度关系在物质的量n一定的情况下。
8、根据四个经验定律推出来的 根据波义耳定律,温度一定,P和V成反比 根据查理定律,P一定,V和T成反比 根据盖吕萨克定律,V一定, P和T成正比 可以导出PVT=k 然后,根据阿佛加德罗定律,PVT都相同时,n也相同,所以可以把上式改写为PVT=nk’,后来把k’成为理想气体常数,就成了PV=nRT了。
9、绝热可逆膨胀,理想气体设CpCv=γ PV^γ=C常数PV=nRT,P随T变化关系P^1γ×T^γ=C常数克拉伯龙方程 dPdT=ΔHT×ΔV。
10、通过克拉伯龙方程退出来的PV=nRT克拉伯龙方程 其中P压强 V气体体积 n气体物质的量 R常数不用管,目前用不到T温度 再联立n=mM m是气体的质量,M是气体的摩尔质量就可以得出上述推论 我建议还是把推论记熟做题会快很多我的经验但愿对你有帮助。
11、具体推导过程如下阿佛加德罗研究是理想气体定律,所以理想气体方程式PV的应用= NRT 既 其中P是压力 V是气体体积 n为对应于分子的数目R是一个常数物质的量 T是热力学温度 获得的PV = NRT,其中R是一个常数,使剩余的四个变量 ,知道这两种,都知道其他两个之间的关系 得到推论1。
12、在pV=nRT中,p是指理想气体的压强,V为理想气体的体积,n表示理想气体物质的量,而T则表示理想气体的热力学温度它和摄氏温度t相差27315,即T=27315+t,R为理想气体常数,其与气体种类无关与单位有关如当压强以Pa体积以m3物质的量以mol温度以K为单位时,R=8m3·Pa·。
13、中学化学中,阿伏伽德罗定律占有重要地位利用克拉伯龙方程式PV=nRT,可以推导出阿伏伽德罗定律的相关推论克拉伯龙方程式表示为PV=nRT其中,P表示压强,V表示气体体积,n表示物质的量,T表示绝对温度,R表示气体常数通过克拉伯龙方程式,可以得到以下推论1在相同TPV时,nA=nB,摩尔。
14、编辑本段公式 pV=nRT克拉伯龙方程 1 p为气体压强,单位PaV为气体体积,单位m3n为气体的物质的量,单位mol,T为体系温度,单 理想气体状态方程 位K R为比例系数,数值不同状况下有所不同,单位是Jmol·K 在摩尔表示的状态方程中,R为比例常数,对任意理想气体而言,R是一。
15、克拉珀龙方程式是描述理想气体状态的一个数学表达式,通常写作PV=nRT这个方程的建立基于BoyleMarriote定律CharlesGayLussac定律以及Avogadro定律通过将体积V表示为压力p和温度T的函数V=fp,T,N,并对其进行全微分处理,然后代入BoyleMarriote定律和CharlesGayLussac定律,经过不定积分操作后。
16、主要推论1同温同压下,V1V2=n1n2 2同温同体积时,p1p2=n1n2=N1N2 3同温同压等质量时,V1V2=M2M1 4同温同压同体积时,M1M2=ρ1ρ2 克拉珀龙方程的推导过程以及克拉珀龙方程与阿伏伽德罗定律推论的关系推导pV=nRT V=fp,T,N求V全微分 不定积分。
17、1由克拉伯龙方程pV=nRT,可得分子数密度n0=NV=nV·NA=pRT·NA=1×10^5×602×10^238314×300K=241×10^25个m32单个氧分子质量m0=MNA=32×10^3602×10^23=532×10^26kg3由克拉伯龙方程变形pM=ρRT,可得氧气密度ρ=pM。
转载请注明来自夕逆IT,本文标题:《克拉伯龙方程式pV=nRT的推导过程~谢谢。》

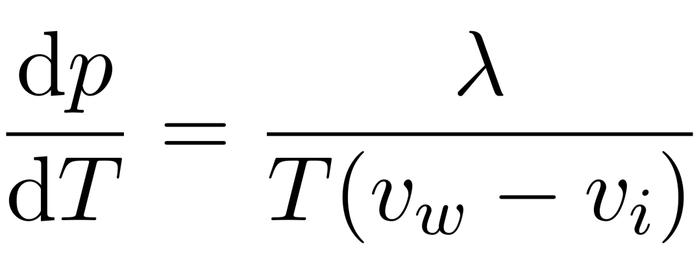
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...